文章目录[+]
当下,人工智能主流的研究方法是连接主义。连接主义学派并不认为人工智能源于数理逻辑,也不认为智能的关键在于思维方式。这一学派把智能建立在神经生理学和认知科学的基础上,强调智能活动是将大量简单的单元通过复杂方式相互连接后并行运行的结果。基于以上的思路,连接主义学派通过人工构建神经网络的方式来模拟人类智能。它以工程技术手段模拟人脑神经系统的结构和功能,通过大量的非线性并行处理器模拟人脑中众多的神经元,用处理器复杂的连接关系模拟人脑中众多神经元之间的突触行为。相较符号主义学派,连接主义学派显然更看重是智能赖以实现的“硬件”。
人类智能的本质是什么?这是认知科学的基本问题。根据自底向上的分析方法,人类智能的本质很大程度上取决于“什么是认知的基本单元”。目前的理论和实验结果表明,要分析认知基本单元,合理的方法既不是物理推理也不是数学分析,而是设计科学实验加以验证。大量的实验结果显示,从被认知的客体角度来看,认知基本单元是知觉组织形成的“知觉物体”。
知觉物体概念的形成具备其特殊的物理基础。脑神经科学研究表明,人脑由大约千亿个神经细胞及亿亿个神经突触组成,这些神经细胞及其突触共同构成了一个庞大的生物神经网络。每个神经细胞通过突触与其他神经细胞进行连接与通信。当通过突触所接收到的信号强度超过某个阈值时,神经细胞便会进入激活状态,并通过突触向上层神经细胞发送激活信号。人类所有与意识及智能相关的活动,都是通过特定区域神经细胞间的相互激活与协同工作而实现的。
作为一个复杂的多级系统,大脑思维来源于功能的逐级整合。神经元的功能被整合为神经网络的功能,神经网络的功能被整合为神经回路的功能,神经回路的功能最终被整合为大脑的思维功能。但巧妙的是,在逐级整合的过程中,每一个层次上实现的都是”1 + 1 > 2”的效果,在较高层次上产生了较低层次的每个子系统都不具备的“突生功能”。这就意味着思维问题不能用还原论的方法来解决,即不能靠发现单个细胞的结构和物质分子来解决。揭示出能把大量神经元组装成一个功能系统的设计原理,这才是问题的实质所在。
研究表明,感觉神经元仅对其敏感的事物属性作出反应。外部事物属性一般以光波、声波、电波等方式作为输入刺激人类的生物传感器,而感觉神经元输出的感觉编码是一种可符号化的心理信息。因此,感觉属性检测是一类将数值信息转化为符号信息的定性操作。感觉将事物属性转化为感觉编码,不仅能让大脑检测到相应属性,还在事物属性集与人脑感觉记忆集之间建立起对应关系,所以感觉属性检测又叫感觉定性映射。神经网络对来自神经元的各简单属性的感觉映象加以组合,得到的就是关于整合属性的感觉映象。比如大脑整合苹果的颜色属性(如红色)和形状属性(如圆形)的感觉映象的结果,得到的就是苹果又红又圆这个整合属性的感觉映象。
在感觉映射下,事物属性结构与其感觉映象结构之间应保持不变,也就是说,感觉映射应该是事物属性集与其感觉记忆集之间的一个同态映射。通常所说的人脑认知是外部世界的反映,就是感觉同态的一种通俗说法。对以上枯燥难懂的文字加以梳理,就是这样一幅图景。人类自从他能被叫做人的那一天起就具备识别物体的能力了:这是剑齿虎,那是长毛象,手里的是棍子。其实剑齿虎也好,长毛象也罢,不过是不同波长不同数量的光子的组合,是我们的视网膜和大脑的视觉皮层把这些光子进一步加工为不同的属性,这就是信息抽象的过程。这种认知可以归结为一个高度抽象化的加工模型。在这个模型中,信息的加工具有从简单到复杂的层次化特征,在每个层次上都有相应的表征,无论是特征提取还是认知加工,都是由不同表征的组合完成的。
表征处理的物质基础是神经元,大量神经元群体的同步活动是实现表征和加工的生理学机制。单个神经元只能表征极为简单的信息,但当它们通过神经电活动有节律的同步震荡整合在一起时,复杂的功能就诞生了。从信息科学的角度看,整个加工过程可以理解为多次特征提取,提取出的特征从简单到复杂,甚至“概念”这种十分抽象的特征也可以被提取出来。但如果人类的认知过程只是提取当前信息的特征并进行分类这么简单的话,它也不值得如此大费笔墨。认知还和注意、情绪等系统有着极强的交互作用,这些功能也和认知密切相关。人的情绪对认知的影响绝非中晚期才启动的高级过程,它的作用远比我们想象的基础得多。焦虑症、抑郁症等情感疾病的患者与不受这些情感疾病困扰的人相比,对负性情绪信息有注意偏向,对带有负面色彩的情绪刺激更容易关注,这种注意偏向发生在视觉感知的早期阶段,其具体机理至今还笼罩在迷雾之中。
从物质基础的角度看,人类智能是建立在有机物基础上的碳基智能,而人工智能是建立在无机物基础上的硅基智能。尽管人工神经网络模拟的是人类神经系统的工作方式,但它归根结底是一套软件,而不是像神经元一样的物质实体,依然要运行在通用的计算机上,所以人工神经网络也属于硅基智能的范畴。
碳基智能与硅基智能的本质区别在于架构,正是架构决定了数据的传输与处理是否能够同时进行。今日计算机的基础是半个多世纪之前诞生的冯·诺伊曼结构体系,而冯·诺伊曼结构体系的一个核心特征是运算单元和存储单元的分离,两者由数据总线连接。运算单元需要从数据总线接收来自存储单元的数据,运算完成后再将运算结果通过数据总线传回给存储单元。这样一来,数据的传输与处理就无法同步进行,运算单元和存储单元之间的性能差距也限制了计算机的整体表现。
数据并非为了存储而存储,而是为了在需要时能够快速提取而存储,归根到底存储的作用是提升数据处理的有效性。遗憾的是,这显然不是计算机的强项。虽然处理器的处理速度和硬盘的容量增势迅猛,但数据总线的传输速度依然是电脑性能的瓶颈:数据不能被即时地送到它该去的地方。由此看来,今日计算机对存储的追求甚至有些舍本逐末。
相比之下,在人类和老鼠等其他哺乳动物的大脑中,数据的传输和处理都由突触和神经元之间的交互完成。重要的是,数据的传输和处理是同步进行的,并不存在先传输后处理的顺序。在同样的时间和空间上,哺乳动物的大脑就能够在分布式的神经系统上交换和处理信息,这绝对是计算机难以望其项背的。此外,人的记忆过程也不仅仅是数据存储的过程,还伴随着去粗取精的提炼与整合。记忆的过程在某种意义上更是忘记的过程,是保留精华去除糟粕的过程。一个聪明人也许会忘记知识中的大量细节,但一定会记住细节背后的规律。碳基大脑的容量恐怕永远也无法和硅基硬盘相比,但是其对数据的使用效率同样是硅基硬盘难以企及的。
1943 年,美国芝加哥大学的神经科学家沃伦·麦卡洛克和他的助手沃尔特·皮茨发表了论文《神经活动中思想内在性的逻辑演算》(A Logical Calculus of Ideas Immanent in Nervous Activity),系统阐释了他们的想法:一个极度简化的机械大脑。麦卡洛克和皮茨首先将神经元的状态二值化,再通过复杂的方式衔接不同的神经元,从而实现对抽象信息的逻辑运算。正是这篇论文宣告了人工神经网络的呱呱坠地,它传奇的故事自此徐徐展开。
与生理学上的神经网络类似,麦卡洛克和皮茨的人工神经网络也由类似神经元的基本单元构成,这一基本单元以两位发明者的名字命名为“MP 神经元(MP neuron)”。大脑中的神经元接受神经树突的兴奋性突触后电位和抑制性突触后电位,产生出沿其轴突传递的神经元的动作电位;MP 神经元则接受一个或多个输入,并对输入的线性加权进行非线性处理以产生输出。假定 MP 神经元的输入信号是个 N+1 维向量 (x0,x1,⋯,xN),第 i 个分量的权重为 wi,则其输出可以写成
上式中的 x0 通常被赋值为 +1,也就使 w0 变成固定的偏置输入 b。
MP 神经元中的函数 ϕ(⋅) 被称为传递函数,用于将加权后的输入转换为输出。传递函数通常被设计成连续且有界的非线性增函数,但在 MP 神经元中,麦卡洛克和皮茨将输入和输出都限定为二进制信号,使用的传递函数则是不连续的符号函数。符号函数以预先设定的阈值作为参数:当输入大于阈值时,符号函数输出 1,反之则输出 0。这样一来,MP 神经元的工作形式就类似于数字电路中的逻辑门,能够实现类似“逻辑与”或者“逻辑或”的功能,因而又被称为“阈值逻辑单元”。
MP 神经元虽然简单实用,但它缺乏一个在人工智能中举足轻重的特性,也就是学习机制。1949 年,加拿大心理学家唐纳德·赫布提出了以其名字命名的“赫布理论”,其核心观点是学习的过程主要是通过神经元之间突触的形成和变化来实现的。通俗地说,两个神经细胞之间通过神经元进行的交流越多,它们之间的联系就会越来越强化,学习的效果也在联系不断强化的过程中逐渐产生。
从人工神经网络的角度来看,赫布理论的意义在于给出了改变模型神经元之间权重的准则。如果两个神经元同时被激活,它们的权重就应该增加;而如果它们分别被激活,两者之间的权重就应该降低。如果两个结点倾向于同时输出相同的结果,两者就应具有较强的正值权重;反过来,倾向于输出相反结果的结点之间则应具有较强的负值权重。
遗憾的是,赫布的学习机制并不适用于 MP 神经元,因为 MP 神经元中的权重 wi 都是固定不变的,不能做出动态的调整。幸运的事,会学习的神经元模型并没有让人等待太久。1957 年,任职于美国康奈尔大学航天实验室的心理学家弗兰克·罗森布拉特受到赫布理论的启发,提出了著名的“感知器(perceptron)”模型。
感知器并不是真实的器件,而是一种二分类的监督学习算法,能够决定由向量表示的输入是否属于某个特定类别。作为第一个用算法精确定义的神经网络,感知器由输入层和输出层组成。输入层负责接收外界信号,输出层是 MP 神经元,也就是阈值逻辑单元。每个输入信号(也就是特征)都以一定的权重被送入 MP 神经元中,MP 神经元则利用符号将特征的线性组合映射为分类输出。
给定一个包含若干输入输出对应关系实例的训练集时,感知器引入了学习机制,能够通过权重的调整提升分类的效果,其具体的学习步骤为:1. 初始化权重 w(0) 和阈值,其中权重可以初始化为 0 或较小的随机数;2. 对训练集中的第 j 个样本,将其输入向量 xj 送入已初始化的感知器,得到输出 yj(t);3. 根据 yj(t) 和样本 j 的给定输出结果 dj,按以下规则更新权重向量(0≤i≤n);4. 重复以上两个步骤,直到训练次数达到预设值。式中的正常数 0<η≤1 被称为学习率参数,是修正误差的一个比例系数。
显然,第三步要对感知器的权重进行更新,是学习算法的核心步骤。这一步的作用在于评估不同输入对分类精确度的影响。如果分类结果和真实结果相同,则保持权重不变;如果不同,就需要具体情况具体分析:如果输出值应该为 0 但实际为 1,就要减少 xj 中输入值为 1 的分量的权重;如果输出值应该为 1 但实际为 0,则要增加 xj 中输入值为 1 的分量的权重。
感知器能够学习的前提是它具有收敛性。罗森布拉特证明了当输入数据线性可分时,感知器学习算法能够在有限次的迭代后收敛,并且得到的决策面是位于两类之间的超平面。本质上讲,在执行二分类问题时,感知器以所有误分类点到超平面的总距离作为损失函数,用随机梯度下降法不断使损失函数下降,直到得到正确的分类结果。
除了优良的收敛性能外,感知器还有很多优点。首先是非参数化特性,即没有做出任何关于固有分布形式的假设,只是通过不同分布重叠区域产生的误差来运行,这意味着即使输入数据是非高斯分布时,算法依然能够正常工作。其次是自适应性,只要给定训练数据集,算法就可以基于误差修正自适应地调整参数而无需人工介入,这无疑在 MP 神经元的基础上前进了一大步。
综上所述,作为神经网络的基础,感知器通过传递函数确定输出,神经元之间通过权重传递信息,权重的变化则根据误差来进行调节。由此,神经网络实现了最基础的学习过程,标志着人工神经网络开始蹒跚学步。
虽然感知器的形式简洁优雅,但它的应用范围也相当有限:只能解决线性分类问题。所谓线性分类意指所有的正例和负例可以通过高维空间中的一个超平面完全分开而不产生错误。如果一个圆形被分成一黑一白两个半圆,这就是个线性可分的问题;可如果是个太极图的话,单单一条直线就没法把黑色和白色完全区分开来了,这对应着线性不可分问题。感知器对于线性不可分问题无能为力。如果训练数据集不是线性可分的,也就是正例不能通过超平面与负例分离,那么感知器就永远不可能将所有输入向量正确分类。在这种情况下,标准学习算法下不会产生“近似”的解决方案,而是出现振荡,导致算法完全失败。
批判感知器最有名的大字报就是所谓的“异或”问题。异或操作是一种两输入的逻辑操作:当两个输入不同时,输出为真;而当两个输入相同时,输出为假。异或操作可以放在包含四个象限的平面直角坐标系下观察:在第一象限和第三象限中,横坐标和纵坐标的符号相同;而在第二象限和第四象限中,横坐标和纵坐标的符号相反。这样一来,一三象限上的两个点 (1, 1) 和 (-1, -1) 就可以归为一类,二四象限上的两个点 (-1, 1) 和 (1, -1) 则可以归为另一类。划分这四个点就是一个二分类问题。这个问题不是一个线性分类问题,因为找不到任何一条直线能将将正方形中两组对角线上的顶点分为一类。1969 年,新科图灵奖得主马文·明斯基和他的麻省理工学院同侪塞默尔·帕波特合著了《感知器:计算几何简介》(Perceptrons: An Introduction to Computational Geometry)一书,系统论证了感知器模型的两个关键问题。第一,单层感知器无法解决以异或为代表的线性不可分问题;第二,受硬件水平的限制,当时的计算机无法完成训练感知器所需要的超大的计算量。
明斯基的著作对感知器无疑是致命的打击。异或问题是最简单的逻辑问题之一,如果连异或的分类都无法解决,这样的模型存在的意义就颇为有限了。于是,政界对神经网络的热情被这一盆冷水浇了个透心凉,这直接导致了科研经费的断崖式下跌;而学界则视人工神经网络研究为洪水猛兽,避之不及。连接主义学派的第一波凛冬就此到来。只是在学术争鸣背后,明斯基的所作所为更藏着些文人相轻的意味。罗森布拉特其人性格张扬,于区区 34 岁的年纪提出感知器模型后更加受人追捧,俨然一副学术网红的模样。更重要的是,大量来自政府的经费都涌向罗森布拉特的项目,也许这才是让明斯基不爽的真正原因。此外,明斯基和罗森布拉特求学路上的交集也暗示着两人之间的纠葛冰冻三尺,绝非一日之寒。
感知器的问题给了明斯基釜底抽薪的契机。在 1969 年版《感知器》中,明斯基不仅论证了感知器在科学上的局限,更夹带了不少对罗森布拉特进行人身攻击的私货。罗森布拉特对感知器在符号处理方面的局限心知肚明,但他万万没想到这些缺陷会被明斯基以如此敌意而致命的方式呈现出来。1971 年,罗森布拉特在 43 岁生日当天划船时意外淹死,至于这究竟是意外事故还是以死明志,恐怕只有他自己知道了。
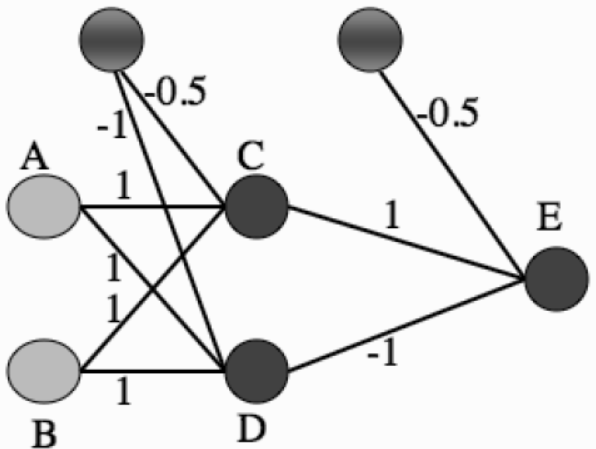
虽然异或问题成为感知器和早期神经网络的阿喀琉斯之踵,但它并非无解的问题。恰恰相反,解决它的思路相当简单,就是将单层感知器变成多层感知器。下图就是一个多层感知器的实例,这个包含单个隐藏层的神经网络能够完美地解决异或问题。
假定两个输入节点 A 和 B 的二进制输入分别为 1 和 0,则根据图中的权重系数可以计算出神经元 C 的输入为 0.5,而神经元 D 的输入为 0。在由 C 和 D 构成的隐藏层中,由于 C 的输入大于 0,因而符号函数使其输出为 1;由于 D 的输入等于 0,符号函数则使其输出为 0。在输出节点的神经元 E 上,各路输入线性组合的结果为 0.5,因而 E 的输出,也是神经网络整体的输出,为 1,与两个输入的异或相等。在此基础上可以进一步证明,这个神经网络的运算规则就是异或操作的运算规则。
多层感知器(multilayer perceptron)包含一个或多个在输入节点和输出节点之间的隐藏层(hidden layer),除了输入节点外,每个节点都是使用非线性激活函数的神经元。而在不同层之间,多层感知器具有全连接性,即任意层中的每个神经元都与它前一层中的所有神经元或者节点相连接,连接的强度由网络中的权重系数决定。多层感知器是一类前馈人工神经网络(feedforward neural network)。网络中每一层神经元的输出都指向输出方向,也就是向前馈送到下一层,直到获得整个网络的输出为止。多层感知器的训练包括以下步骤:首先确定给定输入和当前权重下的输出,再将输出和真实值相减得到误差函数,最后根据误差函数更新权重。在训练过程中,虽然信号的流向是输出方向,但计算出的误差函数和信号传播的方向相反,也就是向输入方向传播的,正因如此,这种学习方式得名反向传播(backpropagation)。反向传播算法通过求解误差函数关于每个权重系数的偏导数,以此使误差最小化来训练整个网络。
在反向传播算法中,首先要明确误差函数的形式。当多层感知器具有多个输出时,每个分类结果 yj 与真实结果 dj 之间都会存在误差。在单层感知器中,误差直接被定义为两者之间的差值。但在多个输出的情形下,如果第一个输出神经元的误差大于零,第二个输出神经元的误差小于零,这两部分误差就可能部分甚至完全抵消,造成分类结果准确无误的假象。如何避免这个问题呢?
为了避免这个问题,在反向传播算法中,每个输出神经元的误差都被写成平方项的形式,整个神经网络的误差则是所有输出神经元的误差之和。如此一来,误差函数就以二次型的形式体现,也就避免了符号的影响。明确定义了误差函数后,就要想方设法让它取得最小值。影响误差函数的因素无外乎三个:输入信号、传递函数和权重系数。输入信号是完全不依赖于神经网络的外部信号,无法更改;传递函数在网络设计过程中已经确定,同样无法更改;所以在算法执行的过程中,能够更新的就只有权重系数了。
既然提到了传递函数,就有必要对多层感知器中的传递函数加以说明。单层感知器中使用的符号函数有一个缺点:它是不连续的函数,因而不能在不连续点上求解微分。为了解决这个弊端,多层感知器采用对数几率函数作为传递函数。还记得对数几率函数在哪里出现过吗?没错,在机器学习中的逻辑回归算法当中。你可以回忆一下对数几率函数的表达式。根据最优化理论,求解误差函数的最小值就要找到误差函数的梯度,再根据梯度调整权重系数,使误差函数最小化。对误差函数的求解从输出节点开始,通过神经网络逆向传播,直到回溯到输入节点。这背后的原理在于权重系数的变化对输出的影响方式并非直接修改,而是通过隐藏层逐渐扩散。这样环环相扣的作用方式体现在数学上就是求导的链式法则。
链式法则是个非常有用的数学工具,它的思想是求解从权重系数到误差函数这个链条上每一环的作用,再将每一环的作用相乘,得到的就是链条整体的效果。利用链式法则求出梯度后,再以目标的负梯度方向对权重系数进行调整,以逐渐逼近误差函数的最小值。将平方误差函数、对数几率函数、求导链式法则三大法宝放在一起,就可以召唤出反向传播算法的流程:
初始化网络中所有权重系数和阈值;在前向计算中,将训练样本送入输入节点,在输出节点得到训练结果,再以平方误差形式计算训练输出和真实输出之间的误差函数
在反向计算中,计算神经网络的局域梯度
并根据局域梯度和学习率 η 从输出层到隐藏层对权重系数进行逐层更新
利用新样本训练多层感知器,迭代进行前向计算和反向计算,直到满足停止准则。
抛开冗杂的数学符号和运算不论,反向传播算法的原理其实并没有那么复杂。如果你能在头脑中勾勒出包含单个隐藏层的多层感知器结构,那不妨直观想象一下当某个输入上出现细微的扰动会导致什么结果?
抛开冗杂的数学符号和运算不论,反向传播算法的原理其实并没有那么复杂。如果你能在头脑中勾勒出包含单个隐藏层的多层感知器结构,那不妨直观想象一下当某个输入上出现细微的扰动会导致什么结果?由于层与层之间的连接方式是全连接,因而单个输入的微小变化会传递到所有的隐藏神经元,每个隐藏神经元都会感受到来自输入的波动。由于隐藏神经元的输入是输入信号的线性组合,因而输入端的扰动体现在隐藏神经元上就经过了一重权重系数的放大。经过权重系数放大后的扰动又被送入非线性的传递函数里,传递函数输入端的扰动导致的输出端的改变就要再乘以一个传递函数的导数作为放大因子。
上面的这个过程发生在单个的隐藏神经元上,而在隐藏层中每个神经元上发生的都是同样的故事,所以整个网络的输出变化就等于所有隐藏神经元上由“权重系数 + 传递函数”计算出的输出变化的总和。不难看出,误差函数对单个输入的偏导数就是“权重系数 + 传递函数”的联合作用。看到这儿你可能会问,说的这些都是输入信号的扰动对输出结果的影响方式,这和反向传播有什么关系呢?当然有啦!当输入信号不变时,两个导数之间的关系就完全由权重系数的变化决定。将上面过程中输入信号和权重系数的角色做个调换,就可以得出误差函数对权重系数的偏导数就是“输入信号 + 传递函数”的联合作用。而这,恰恰就是链式法则的原理。
多层感知器的核心结构就是隐藏层,之所以被称为隐藏层是因为这些神经元并不属于网络的输入或输出。在多层神经网络中,隐藏神经元的作用在于特征检测。随着学习过程的不断进行,隐藏神经元将训练数据变换到新的特征空间之上,并逐渐识别出训练数据的突出特征。在解决实际问题时,多层感知器的设计要考虑一些工程因素。假设单隐层的多层感知器有 L 个输入节点、M 个隐藏节点和 N 个输出节点,那这个网络的权重系数总数就是 (L+1)×M+(M+1)×N。这些权重的取值都需要由反向传播算法确定,而反向传播算法又由训练数据的错误来驱动。因而用于训练的数据越多,多层感知器的学习效果也就越好。一个经验法则是训练样本数目应该是权重系数数目的 10 倍,这显然对计算能力提出了较高的要求。从这个角度看,明斯基对感知器的批评是站得住脚的。
抛开训练数据量不论,隐藏层和隐藏神经元的数目也是网络设计中需要考虑的问题。在数学上可以证明,单个隐藏层就能够实现凸区域,双隐藏层更是可以实现任意形状的凸区域,也就能够解决任何复杂的分类问题。在隐藏层数目不变的前提下,区域的复杂程度还能够随着隐藏神经元数目的增加而提升。在数学上同样可以证明,只要隐藏神经元的数目足够多,一个隐藏层就能使多层感知器以任意精度逼近任意复杂度的连续函数。通常情况下,多层感知器不会选择两个以上的隐藏层,因为层数越多,要追踪哪些权重正在被更新就越困难,又不会带来性能的提升。
多层感知器的训练要需要多次遍历整个数据集,因而迭代次数就成为另一个重要的问题。预先设定迭代次数无法保证训练效果,预先设定误差阈值则可能导致算法无法终止。因而常用的办法是:一旦误差函数停止减小,就终止学习算法。同其他机器学习方法一样,多层感知器也面临过拟合的风险。模型的泛化能力可以通过验证集来监督,也就能够在一定程度上避免过拟合的发生。当训练集的误差下降但验证集的误差上升时让训练立即停止,这就是所谓“早停”的过拟合抑制策略。当然,正则化方法也可以应用在多层感知器的训练中。
多层感知器是一类全局逼近的神经网络,网络的每个权重对任何一个输出都会产生同等程度的影响。因而对于每次训练,网络都要调整全部权值,这就造成全局逼近网络的收敛速度较慢。显然,这是一种牵一发而动全身的全局作用方式。与全局作用对应的是局部作用。在局部作用中,每个局部神经元只对特定区域的输入产生响应。如果输入在空间上是相近的,对这些输入的反应应该是相似的,那么被这些输入激活的神经元也应该是同一批神经元。进一步推广又可以得到,如果一个输入 A 在另外两个输入 B1 和 B2 的空间位置之间,那么响应输入 B1 和 B2 的神经元也应该在一定程度上被 A 激活。
神经元的局部作用原理有它的生理学依据。当你仰望夜空中的点点繁星时,茫茫暗夜中的星光激活的是视觉神经的特定部分。随着地球的自转,星光也会移动,虽然亮度没有变化,但不同位置的星光激活的就是视觉神经中的不同部分,因而产生响应的神经元也会发生变化。有些原本被激活的神经元会因为目标对象的移出而被抑制,有些原本被抑制的神经元则因为目标对象的移入而被激活。在神经科学中,这个概念被称为“感受野(receptive field)”。一个感觉神经元的感受野指的是位于这一区域内的适当刺激能够引起该神经元反应的区域。人类神经的感受野的变化方式可以在人工神经网络中以权重系数的形式体现出来,而按照感受野的变化规律设置权重系数,得到的就是“径向基函数神经网络”(Radial Basis Function Network , RBFN)。
径向基网络通常包含三层:一个输入层、一个隐藏层和一个输出层。其中隐藏层是径向基网络的核心结构。每个隐藏神经元都选择径向基函数作为传递函数,对输入分量的组合加以处理。需要注意的是,输入节点和隐藏节点之间是直接相连的,权重系数为 1。径向基函数是只取决于与中心矢量的距离的函数,也就是不管不同的点是在东西还是南北,只要它们和中心点之间的距离相同,其函数值就是相同的。径向基函数的图形会根据确定的中心点呈现圆周对称的性质。如果将欧氏距离作为距离的度量,函数的形式就可以定义为平缓变化的高斯函数,其表达式就是
式中的每个中心向量 wi 都是径向基网络中的权重系数。一般情况下,所有高斯函数会共享同一个带宽 σ,因而将不同隐藏单元区分开来的就是中心向量wi。每个径向基函数的输出按照参数进行线性组合后,再被送到输出神经元加以处理。输出神经元通常是普通的 MP 神经元。前面介绍的是径向基网络的生理学依据,下面让我们看看这套方法在数学上的意义。隐藏层的作用是实现从输入空间到非显式特征空间的非线性变换,由此,低维空间上的非线性可分数据就被映射到高维空间之中。在一定的条件下,转换后的数据变为线性可分的可能性很高,这一点已经在数学上得到证明。
看到这里,你是否有似曾相识的感觉呢?没错,这和支持向量机的思路是一样的!支持向量机中的核技巧能够把低维空间中的非线性问题映射成高维空间中的线性问题,将低维空间中曲面形式的决策边界转化为高维空间中的超平面,从而降低分类问题的难度。在支持向量机中常用的核函数就包括高斯核函数,回忆一下,它的形式是不是和径向基网络中的高斯函数形式一模一样呢?将低维问题投射到高维空间是解决线性不可分问题的通用方法。但是在某些情况下,一个非线性映射就足以在低维空间中解决问题,而不需要升高隐藏空间的维数,提升算法的复杂度。高斯函数就是这类“杀鸡焉用宰牛刀”的实例。
还是以异或问题为例。在异或问题中,四个数据点 (0, 0), (0, 1), (1, 0), (1, 1) 是正方形的四个顶点,处于对角线方向上的两个点属于同一个模式。如果引入高斯函数 Φi(x)=exp(−∣∣x−ui∣∣2),i=1,2,其中 u1=[0,0],u2=[1,1],则原始的四个数据点就被变换为 (0.1353, 1), (0.3678, 0.3678), (0.3678, 0.3678), (1, 0.1353)。经过高斯函数的变换后,(0, 1) 和 (1, 0) 两个具有相同异或结果的点重合在一起,异或问题也变成了线性可分问题。但在之前的处理中,空间的维数并未增加,问题的转化只用到了非线性的高斯函数。
另一个理解径向基网络的角度是多变量插值。整体上看,径向基网络的作用是学习一个高维空间上的超曲面,根据训练数据进行训练的过程就是对超曲面进行拟合的过程。但由于数据中存在噪声,因而训练得到的结果还需要泛化处理,泛化的任务就是在数据点之间进行插值,使插值后的曲面仍然要经过所有数据点。在插值过程中,使用的插值函数就是不同类型的径向基函数。训练数据中的每个样本都是新的高维空间中的一个点,插值要做的是把所有离散的点连成一片,形成一个曲面。那么插值操作具体是如何进行的呢?高斯形式的径向基函数将每个训练样本映射为一个连续的函数,函数的中心就是样本点的取值。在整个空间内对所有的高斯函数求和,得到的就是拟合出的曲面。
当新样本出现时,其在曲面上的映射值就等于所有高斯径向基函数在这个数据点上的函数值之和。感受野理论告诉我们,每个训练数据对曲面的影响都只限于其数据周边的一个小范围内,因而在新样本的插值结果中,贡献较大的是离它比较近的训练数据。如果某些训练数据距离新样本较远,就不会对新样本产生影响。在实际应用中,对径向基网络的训练包括两个步骤。第一步的任务是初始化中心向量 wi 的位置,中心向量的位置既可以随机分配,也可以通过 K 均值聚类这一无监督学习的方法完成。这个步骤对应的是隐藏层的训练。第二步的任务是用线性模型拟合初始化的隐藏层中的各个中心向量,拟合的损失函数设定为最小均方误差函数,使用递归最小二乘法(Recursive Least Square)使损失函数最小化。这个步骤对应的是对输出层的训练。
使用 K 均值算法训练隐藏层时,聚类的数目 K 决定了隐藏神经元的数目,通过这个参数设计者可以控制径向基网络的性能和计算复杂度。算法的参数确定后,就能够对训练数据进行无监督的分类,计算出的每个聚类的中心就是高斯函数的中心。出于简化设计的考虑,每个高斯函数的带宽都是相同的,并被统一设置为
其中 dmax 是不同中心之间的最大距离。这种带宽的配置符合 K 均值算法中的中心散布,保证了各个高斯函数既不会太宽也不会太窄。隐藏层的训练完成后,就可以开始输出层的训练了。输出层的输入信号是每个隐藏神经元输出信号的线性组合,因而递归最小二乘法是训练权重向量的合适选择。权重向量和隐藏神经元输出之间的关系可以表示为
式中的 R 表示 K 个隐藏神经元输出之间的相关矩阵,w^ 表示待训练的未知权重向量,r 表示期望响应和隐藏单元输出之间的 K×1 维互相关向量,自变量 n 则代表了训练的轮次。递归最小二乘法的作用在于简化逆矩阵 R−1(n) 的求解,其详细的推导过程在此就不介绍了。
在训练完成后还可以添加额外的一个步骤,利用反向传播算法对径向基网络的所有参数进行一次微调,以达到更好的训练效果。这是由于无论是 K 均值聚类还是递归最小二乘法,都是针对特定层次的优化,反向传播优化的对象则是作为整体的径向基网络,它可以在统计意义上保证了整个系统的最优性。与感知器类型的神经网络相比,径向基网络代表的则是局部逼近的工作方式。神经元的输入离径向基函数中心越近,神经元的激活程度就越高。但两者都能够实现通用逼近(universal approximation),也就是对任意非线性函数的逼近。
无论是全局逼近的多层感知器,还是局部逼近的径向基网络,在训练中用到的都是监督学习的方法。如果将无监督学习引入神经网络中,对应的结构就是自组织特征映射(Self-Organizing Map),这是芬兰赫尔辛基大学的泰乌沃·柯霍宁于 1981 年提出的一类神经网络。相比于前面介绍的神经网络,自组织映射有两个明显的不同。
第一,它能够将高维的输入数据映射到低维空间之上(通常是二维空间),因而起到降维的作用。在降维的同时,自组织映射妙就妙在还能维持数据在高维空间上的原始拓扑,将高维空间中相似的样本点映射到网络输出层的邻近神经元上,从而保留输入数据的结构化特征。第二,自组织映射采用的是竞争性学习而非传统的纠错学习。在竞争性学习中,对输入样本产生响应的权利并不取决于预设的权重系数,而是由各个神经元相互竞争得到的。不断竞争的过程就是网络中不同神经元的作用不断专门化的过程。
竞争性学习的理念来自于神经科学的研究。在生物的神经系统中存在着一种名叫“侧向抑制”的效应,它描述的是兴奋的神经元会降低相邻神经元活性的现象。侧向抑制能够阻止从侧向刺激兴奋神经元到邻近神经元的动作电位的传播。什么意思呢?当某个神经元受到刺激而产生兴奋时,再刺激相近的神经元,则后者的兴奋对前者就会产生抑制作用。这种抑制作用会使神经元之间出现竞争,在竞争中胜出的神经元就可以“胜者通吃”,将竞争失败的神经元全部抑制掉。自组织映射中的竞争性学习模拟的就是上述的侧向抑制机制。自组织映射的拓扑结构并非如多层感知器般的层次结构,而是一张一维或者二维的网格,网格中的每个节点都代表一个神经元,神经元的权重系数则是和输入数据的维度相同的向量。在拓扑结构中,每个神经元的位置都不是随意选取的,而是和功能有着直接的关系。距离较近的神经元能够处理模式相似的数据,距离较远的神经元处理对象的差异也会很大。
由于神经元在网格中的位置至关重要,因而训练过程就是在空间上对神经元进行有序排列的过程。自组织映射为神经元建立起一个坐标系,由于每个网格神经元对应一类特定的输入模式,输入模式的内在统计特征就是通过神经元的坐标来表示的。因此,自组织映射的主要任务就是将任意维度的输入模式转换为一维或二维的离散映射,并以拓扑有序的方式自适应地实现这个映射。在训练过程中,自组织映射中每个神经元的权重系数首先要初始化,初始化的方式通常是将其赋值为较小的随机数,这可以保证不引入无关的先验信息。当初始化完成后,网络的训练就包括以下三个主要过程。
竞争过程:对每个输入模式,网络中的神经元都计算其判别函数的取值,判别函数值最大的神经元成为竞争过程的优胜者;合作过程:获胜神经元决定兴奋神经元的拓扑邻域的空间位置;自适应过程:兴奋神经元适当调节其权重系数,以增加它们对于当前输入模式的判别函数值,强化未来对类似输入模式的响应。
竞争过程的实质是找到输入模式和神经元之间的最佳匹配。由于输入模式 x 和权重系数 w 是具有相同维度的向量, 因而可以计算两者的内积作为判别函数。在线性代数中我曾提到,内积表示的是向量之间的关系,两个归一化向量的相关度越高,其内积也就越大。因而通过选择具有最大内积 wjTx 的神经元,就可以决定兴奋神经元拓扑邻域的中心位置。两个向量的内积越大,它们之间的欧氏距离就越小,因而内积最大化的匹配准则等效于欧氏距离最小化。从这个角度看,获胜神经元就是对输入模式的最佳匹配。
竞争过程确定了合作神经元的拓扑邻域的中心,合作过程就要界定中心之外的拓扑邻域。借鉴侧向抑制效应,自组织映射中的拓扑邻域被定义成以最佳匹配神经元和兴奋神经元之间的侧向距离为自变量的单峰函数。由于神经元在传导时倾向于激活距离较近的神经元,因而拓扑邻域的幅度在距离为 0 的中心点取到最大值,并随着侧向距离的增加而单调衰减。同时,拓扑邻域还应该满足平移不变性,也就是邻域幅度不依赖于中心点的位置。除了单峰值和平移不变性之外,自组织映射中的拓扑邻域还有另一个特点,就是其大小会随着时间的推移而收缩,也就是幅度值随着时间的增加而下降。这个时变性质的意义在于逐渐减少需要更新的神经元的数量。
网络的自组织特性要求神经元的权重系数具备自动调节的功能。权重系数的整体变化趋势是向数据靠拢,因而其分布也将趋于输入模式的分布。权重系数的更新方程如下所示
式中的 η(n) 是随时间增加而下降的学习率参数,hj,i(x)(n) 则是拓扑邻域函数。
因而,自适应过程可以分为两个阶段。第一阶段是排序阶段,权重系数的拓扑排序在这个阶段形成;第二阶段是收敛阶段,通过微调特征映射实现对输入模式的精确描述。只要算法的参数没有问题,自组织映射就能将完全无序的初始状态按照输入模式以有组织的方式重构,这也是“自组织”的含义。
由于自组织映射采用的是迭代的训练方法,初始值的好坏便至关重要。传统算法采用的是随机方式的初始化,后来又提出了基于主成分的初始化方法。事实上,初始化方法的性能取决于输入数据集的几何形状。如果数据集在主成分上的投影是线性的,就应该选择主成分初始化。可对于非线性数据集而言,随机初始化反而是最优选择。
综合起来,自组织映射的训练算法可以归纳为以下几个步骤:使用主成分法或随机法初始化神经元的权重系数;选取训练集中的样本用于激活整个网络;根据最小距离准则寻找最佳匹配神经元;通过更新方程调整所有神经元的权重系数;重复以上步骤直到在从输入模式到神经元的映射关系中观察不到明显变化。
从输入模式到神经元的映射关系被称为特征映射,它具有很多良好的性质。由于权重系数的维度会远远小于输入数据的可能数目,因而特征映射可以对输入空间提供一个良好的近似,起到数据压缩的作用。从这个角度理解,自组织映射可以看成是一个编码器 - 解码器模型:寻找最佳匹配神经元就是对输入模式进行编码,确定权重系数则是对编码结果进行解码,邻域函数则可以表示对编解码过程造成干扰的噪声的概率密度。自组织映射的这个性质与信息论中用于数据压缩的向量量化方法不谋而合。
当算法收敛后,特征映射就能够表示出输入模式的统计特性。如果输入空间上的某些数据出现的概率较高,它们就会被映射到输出空间中更大的区域上,也就会涵盖更多的神经元。但这个趋势只有定性的意义,自组织映射不能给出输入数据固有概率分布的精确表示,因而不具备定量描述的能力。虽然不能定量描述固有分布,但自组织映射依然能够选择出一组最优的特征,使这组特征在逼近固有分布时具有最佳的效果。自组织映射通过以无监督方式训练大量数据实现特征映射,以实现不同类型数据的区分。其简便易行的特性和强大的可视化能力使它在不少需要大规模数据训练的应用中得到使用。自组织映射一个典型的应用是在图像处理中检测和描述语义目标和目标类之间的存在关系,以及自然语言中单词的语义规则。
模糊神经网络是一类特殊的神经网络,它是神经网络和模糊逻辑结合形成的混合智能系统,通过将模糊系统的类人推理方式与神经网络的学习和连接结构相融合来协同这两种技术。简单来说,模糊神经网络(fuzzy neural network)就是将常规的神经网络赋予模糊输入信号和模糊权值,其作用在于利用神经网络结构来实现模糊逻辑推理。在生活中,我们在臧否人物时很少给出非黑即白的二元评价。这是因为每个人在生活中都扮演着复杂的多重角色,不是好人就是坏人的评判方式显然有失客观。这就是模糊理论在生活中最直接的体现。正如美国加州大学伯克利分校的洛特菲·扎戴所说:“当系统的复杂性增加时,我们使它精确化的能力将减小。直到达到一个阈值,一旦超越这个阈值,复杂性和精确性将相互排斥。”
1965 年,正是这位洛特菲·扎戴提出了与模糊数学相关的一系列理论,并由此衍生出模糊系统的概念。1988 年,供职于日本松下电气的高木秀幸和小林功提出了将神经网络与模糊逻辑结合的想法,这标志着神经模糊系统(Neuro-fuzzy system)的诞生。神经模糊系统的基础是模糊集合和一组“如果...... 那么......”形式的模糊规则,利用神经网络的非线性和学习机制获得类人的推理能力。1993 年,意大利帕多瓦大学的乔万尼·波尔托兰提出了将多层前馈神经网络模糊化的思路,这就是这里所讨论的模糊神经网络。需要说明的是,模糊神经网络和神经模糊系统是不同的。神经模糊系统的输入和输出都是确定对象。因此在神经模糊系统中,必备的结构是模糊化层和去模糊化层。模糊化层用于将输入的确定对象模糊化,去模糊化层则用于将输出的模糊对象转化为确定对象。相比之下,模糊神经网络的输入和输出都是模糊对象,完成的也是模糊推理的功能。
在介绍模糊神经网络之前,有必要对一些基本概念加以解释。模糊理论中最基本的概念是模糊集合。在不模糊的集合里,每个元素和集合之间的隶属关系是明确的,也就是要么属于集合,要么不属于集合,两者之间泾渭分明。可在模糊集合中,元素和集合之间的关系不是非此即彼的明确定性关系,而是用一个叫做隶属度的函数定量表示。在现实中评判某个人物的时候,通常会说他“七分功三分过”或是“三分功七分过”,这里的三七开就可以看成是隶属函数。模糊集合是对“对象和集合之间关系”的描述,模糊数描述的则是对象本身。“人到中年”是很多人愿意用来自嘲的一句话,可中年到底是个什么范围呢?利用排除法可以轻松确定 25 岁算不上中年,55 岁也算不上中年,可要是对中年给出一个明确的正向定义就困难了。因而如果把“中年”看作一个数的话,它就是个模糊数。模糊数在数学上的严格定义是根据模糊集合推导出来的,是个归一化的模糊集合,但通俗地说,模糊数就是只有取值范围而没有精确数值的数。
模糊数可以用来构造模糊数据,对模糊数据进行运算时,依赖的规则叫做扩展原理。对两个确定的数做运算,得到的结果肯定还是一个确定的数。可一旦模糊数参与到运算中来,得到的结果也将变成一个模糊数。扩展原理及其引申得到的模糊算术,定义的就是运算给模糊数的模糊程度带来的变化,这当然也是一个通俗的说法。在模糊算术中,传统的加减乘和内积等运算都被改造成对模糊集合的运算。有了这些概念,就可以进一步解释模糊神经网络。模糊神经网络的拓扑与架构和传统的多层前馈神经网络相同,但其输入信号和权重系数都是模糊集合,因而其输出信号同样是模糊集合。而在网络内部,处理输入信号和权重系数的则是模糊数学,隐藏神经元表示的就是隶属函数和模糊规则。模糊化的处理必然会影响神经网络的特性,因而学习算法的设计和通用逼近特性的保持就成为模糊神经网络要解决的核心问题。
构成模糊神经网络的基本单元是模糊化的神经元。模糊神经元的输入信号和权重系数都是模糊数,传递函数也需要对模糊集合上的加权结果进行处理。模糊神经元的组合形成模糊神经网络。模糊神经网络的训练方式同传统的神经网络类似,即定义一个误差函数并使其最小化。但由于模糊数不能进行微积分的计算,因此不能直接对模糊的权重系数使用反向传播,需要在处理误差时需要针对模糊数的特性提出新的方法。两种常用的方法是基于水平集的方法和基于遗传算法的方法。基于水平集的方法采用的是直接推导的方式,通过确定模糊集合的水平集对模糊数中的元素加以筛选。假如一个模糊数中包含三个元素 x、y 和 z,其参数分别是 0.3、0.6 和 0.7,那么当截断点等于 0.5 时,这个模糊数的 0.5 水平集就会把参数为 0.3 的元素 x 过滤掉,只保留参数大于 0.5 的 y 和 z。在神经网络的训练中,训练算法的作用就是通过计算偏导数和应用反向传播算法,优化每个水平集的截断点,从而确定模糊权值。
水平集方法的致命缺陷在于缺乏理论依据,这严重限制了它的应用。一个不加任何限制的模糊数肯定不能用有限个参数来描述,因而要基于水平集方法来设计通用的模糊神经网络学习算法是不可能的。当模糊数被限制为三角形或者梯形时,算法可以得到一定的简化。在模糊神经网络的训练中,如果保持学习率参数不变,误差函数就难以快速收敛。即使收敛也可能陷入局部最小值上,在不同的学习率参数下得到不同的局部最小值。为了处理这个问题,模糊神经网络引入了一种叫做“共轭梯度(conjugate gradient)”的机制,使训练过程能够找到全局最优解。而要确定最优的学习率,就要借助遗传算法(genetic algorithm)。
共轭梯度方法比较复杂,在这里不做展开。相比基于水平集的方法,基于遗传算法的方法是摸着石头过河,通过迭代逐步找到误差函数的最小值,从而确定权重系数。但它并没有解决水平集方法的本质问题,适用范围仍然被局限在三角形和梯形这类特殊的模糊数上,纯属换汤不换药的做法。除了学习算法之外,逼近性能也是模糊神经网络设计中的核心问题。传统神经网络可以通过引入少量隐藏层实现对任意问题的逼近,但模糊神经网络能不能达到这个要求尚需证明。受学习算法的限制,对逼近性能的考察也只能针对特定类型的模糊神经网络进行。研究结果表明,当输入和权值都被限定为实数时,四层的前馈网络就足以逼近任意形式的模糊取值函数。这意味着模糊神经网络和传统神经网络的性能是相同的,因为抛去输入层和输出层之外,四层网络就只剩两个隐藏层了。
模糊神经网络是一种混合智能系统,能够同时处理语言信息和数据信息,因而是研究非线性复杂系统的有效工具,也是软计算的核心研究内容之一,在模式识别、系统分析和信号处理等领域都有成功应用的实例。但相对于打了翻身仗的传统神经网络,摆在模糊神经网络面前的依然是雄关如铁的境地。
接下来,我将分享人工智能---深度学习

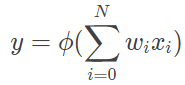
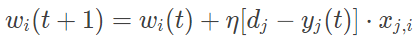
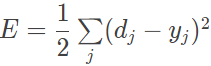
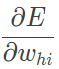
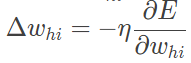

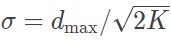
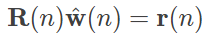
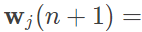
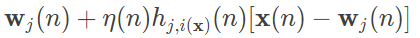



发表评论