文章目录[+]
神经网络是理解深度表征的模型,深度学习是训练深度神经网络的算法,两者是一脉相承的关系。本质上讲,神经网络和深度学习都是由数据驱动的,大量有标记的训练样本是复杂模型取得良好性能的前提,这也解释了为什么直到近年来深度学习才得以蓬勃发展。
早年间的人工智能赖以实现的基础是逻辑学,但逻辑学适用的是理想化的,不存在任何不确定性的世界。可遗憾的是,真实世界是由随机性和误差主宰的,在这光怪陆离的环境中,纯粹的数理逻辑就如同古板的老夫子一般与周遭格格不入。可即使抛开噪声与干扰不论,很多问题也没有固定的解。在医学上,即使子女的基因和母亲的基因已经确定,父亲的基因也可以有多种可能。要解决这类不确定性推理的问题,就必须借助概率论的方法。而将概率方法与图论结合起来,得到的就是今天的主题:概率图模型。
概率图模型(probabilistic graphical model)也叫结构化概率模型,是用图论表现随机变量之间的条件依赖关系的建模方法。典型的概率图模型包括贝叶斯网络和马尔可夫随机场,分别对应着有向图模型和无向图模型。贝叶斯网络(Bayesian network)的拓扑结构是有向无环图,“有向”指的是连接不同顶点的边是有方向的,起点和终点不能调换;“无环”指的是从任意顶点出发都无法经过若干条边回到该点,在图中找不到任何环路。
贝叶斯网络中的顶点表示随机变量,一个顶点既可以表示可观察的显式变量,也可以表示未知参数和隐变量。如果不同的变量之间存在因果关系,那么相应的顶点就会由带箭头的边连接起来,箭头的方向由表示原因的变量指向表示结果的变量,边的权重就是对应的条件概率值。
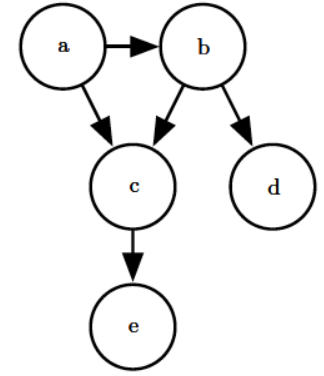
贝叶斯网络的作用是表示出随机变量之间的条件依赖关系,将多个随机变量的联合概率分布分解为条件概率因子乘积的形式。根据条件概率的链式法则,四个随机变量 A,B,C,D 的联合概率可以写成
那么根据上面的概率图,联合概率就可以简化为
不知道这个例子是否让你想起另一种机器学习的方法:朴素贝叶斯分类。朴素贝叶斯分类的基础假设是不同的属性之间条件独立,因此类条件概率可以表示成属性条件概率的乘积。但在绝大多数情形下,这个假设是不成立的。将属性之间的依赖关系纳入后,得到的就是通用的贝叶斯网络。贝叶斯网络引出的一个重要概念是条件独立性(conditionally independence)。如果事件 a 和 b 在另一事件 c 发生时条件独立,就意味着在 c 发生时,a 发生与否与 b 发生与否相互无关,两者联合的条件概率等于单独条件概率的乘积,其数学表达式为
条件独立性可以这样理解,假设天降大雪,那么一对夫妻各自从工作单位回家的话,他们到家的时间都会因下雪而延长,但两个人各自耽误的时间在下雪的条件下是独立的;可如果老公要去接老婆一起回家的话,条件独立性就不再满足了。条件独立性是概率论视角下的概念,如果从图论的角度看,变量之间的依赖与独立对应的是顶点之间的连通与分隔。直观理解,两个直接相连的变量肯定不会条件独立。在不直接相连的两个变量之间,信息必须通过其他变量传递,如果信息传递的通道全部被堵塞,那么两个变量之间就能够满足条件独立性。假设两个变量 X 和 Y 之间通过第三个变量 Z 连接,那么连接的方式可以分为以下三种(注意箭头方向的区别):
顺连:X→Z→Y 或 X←Z←Y分连:X←Z→Y汇连:X→Z←Y
在顺连的情况下,当变量 Z 已知时,X 和 Y 条件独立。这是因为确定的中间变量不能通过变化传递信息,Z 的固定取值不会随 X 的变化而变化,所以 X 的变化自然也不会通过 Z 影响到 Y。这里的变量 Z 就像一扇固定的水闸,隔开了 X 和 Y 之间的流动,也就堵塞了两者之间的信息通道。分连的情况与顺连类似,Z 扮演的同样是固定水闸的角色。分连代表了一因多果的情况,当这个原因确定后,所有的结果之间都不会相互产生影响,因而 Z 已知时,X 和 Y 条件独立。
反过来,在多因一果的汇连情形中,当 Z 未知时,来自 X 和 Y 的信息都会从这个窟窿里漏掉,此时 X 和 Y 条件独立。反过来,Z 已知意味着将这个窟窿堵上,X 和 Y 之间就构造出信息流动的通路,也就不满足条件独立的条件。需要注意的是,这里的 X,Y,Z 既可以是单个的顶点,也可以是顶点的集合。条件独立性又可以引出贝叶斯网络另一个良好的性质,通俗的说就是贝叶斯网络的每个顶点只取决于有箭头指向它的其他顶点,而与没有箭头指向它的其他顶点条件独立。这个性质简化了贝叶斯网络中联合概率分布的计算,也可以节省大量的运算和存储。
当研究者要对真实世界建模时,最理想的方案是建立起包罗万象的联合分布,这就要求计算出分布中所有随机变量的所有可能取值的概率,并将它们存储起来。假定一个模型中包含 8 个二进制的随机变量,需要存储的概率值数目就会达到 28=256 个。可如果在这 8 个变量中,每个变量最多只取决于其他两个变量,那么贝叶斯网络的概率表需要存储的只是相关顶点之间所有可能的状态组合,最多只要计算 8×22=32 个值,这不仅降低了运算复杂度,也节省了存储空间。尤其是在实际问题中,涉及的变量数目可能成千上万时,只要每个顶点都只有少量的父节点,贝叶斯网络在运算上的优势就体现得尤为明显。
贝叶斯网络的另一个优点是能够根据各变量之间的条件依赖性,利用局部分布来求得所有随机变量的联合分布。这个特点让贝叶斯网络在解决复杂问题时不需要关于某个实例的完整知识,而是从小范围的特定知识出发,逐步向复杂问题推广。贝叶斯网络是基于不确定性的因果推断模型,其作用体现在在不完备的信息下,根据已观察的随机变量推断未观察的随机变量。在给定变量之间层次关系的前提下,如果按照自底向上的方式执行推断,就是由果溯因的诊断,这就像医生根据症状诊治病因(诊断过程其实就可以看成基于经验的贝叶斯推理过程);如果按照自顶向下的方式执行推断,就是由因得果的推理,这使得贝叶斯网络可以用作数据的生成模型。
贝叶斯网络的构造包括两个步骤:首先要根据变量之间的依赖关系建立网络的拓扑结构,其次要根据拓扑结构计算每条边上的权重,也就是条件概率。网络结构的构建通常需要特定的领域知识,条件概率表的构造也就是贝叶斯网络的训练,在网络的规模较大时可以使用期望最大化等方法实现。将贝叶斯网络的有向边替换为无向边,得到的就是马尔可夫随机场。马尔可夫随机场(Markov random field)属于无向图模型,它的每个顶点表示一个随机变量,每条边则表示随机变量之间的依赖关系。使用无向边使马尔可夫随机场不能表示出推理关系,但这也解除了对环路结构的限制。环路的存在使它可以表示循环依赖,而这又是贝叶斯网络无法做到的。和贝叶斯网络相比,马尔可夫随机场侧重于表示随机变量之间的相互作用。
贝叶斯网络中每一个节点都对应于一个先验概率分布或者条件概率分布,因此整体的联合分布可以直接分解为所有单个节点所对应的分布的乘积。而在马尔可夫随机场中,由于变量之间没有明确的因果关系,联合概率分布通常会表达为一系列势函数的乘积。这些乘积的求和并不一定等于 1,因而必须进行归一化才能得到有效的概率分布。马尔可夫随机场中的联合概率分布可以写成
式中的每个 xk 代表一个团,团是所有顶点的一个子集,并且团中所有的顶点都是全连接的;fk(⋅) 表示每个团对应的势函数,通常取对数线性模型;Z 表示的则是用于归一化的配分函数。在马尔可夫随机场中,随机变量的独立性和顶点的连通性之间也有对应关系,但其形式却比贝叶斯网络更加简单。要判断两个变量是否独立,只需要观察对应的顶点之间有没有将它们连接在一起的边就可以了。只有在两个顶点之间不存在任意一条信息通路时,对应的随机变量才是条件独立的。条件独立通常意味着两者之间所有的顶点都有固定的观察值。
无论是贝叶斯网络还是马尔可夫随机场,都属于结构化的概率模型。它们提供了将概率模型的结构可视化的简单方式,而对图形的观察可以加深对模型性质的认识,其中最主要的性质就是变量之间的条件独立性。此外,概率图模型还可以表示学习和推断过程中的复杂计算,隐式地承载了图形背后的数学表达,这在以下解决问题的三步框架得以体现。表示:如何对不确定性和随机变量之间的关系进行建模推断:如何从建立的模型中推演出要求解的概率学习:对于给定的数据来说,何种模型是正确的。
梅拉妮·米切尔在《复杂》中举过一个例子:在巴西的亚马逊雨林中,几十万只行军蚁(已知的行为最简单的生物)正在行进。用现在时髦的话说,这是一支去中心化、自组织的大军。在这个蚁蚁平等的团体中,单个蚂蚁几乎没有视力,也不具备什么智能。可聚集成团体的他们组成了扇形的团状,一路风卷残云地吃掉所有能吃掉的,带走所有能带走的。高效的它们只需一天就能消灭雨林里一个足球场面积内的所有食物。到了夜间,蚂蚁会自发形成一个球体,保护起蚁后和幼蚁,天亮后又各就各位,继续行军。快速飞行的蝙蝠群在狭窄的洞穴中互不碰撞,大雁群在飞行时自发地排列成人字形、海洋鱼群通过几何构型充分利用水流的能量...... 这些自然界中的集群行为早早就吸引了人类的注意。在由大量数目的生物个体构成的群体中,不同个体之间的局部行为并非互不相关,而是互相作用和影响,进而作为整体化的协调有序的行为产生对外界环境的响应。生物群体正是通过个体行为之间的互动达到“整体大于部分之和”的有利效果,就像一百只行军蚁只会横冲直撞,一百万只行军蚁却能整齐划一。
实现集群智能的智能体必须能够在环境中表现出自主性、反应性、学习性和自适应性等一系列智能特性,但这并不意味着群体中的个体都很复杂。集群智能的核心是由众多简单个体组成的群体能够通过相互之间的简单合作来实现某些功能,完成某些任务。其中,“简单个体”是指单个个体只具有简单的能力或智能,“简单合作”是指个体与其邻近的个体只能进行某种简单的直接通信或通过改变环境间接与其它个体通信,从而可以相互影响、协同动作。与高大上的深度学习不同,集群智能既不需要汪洋浩瀚的物理数据,也不需要艰深晦涩的数学算法,难道蚂蚁和大雁会计算微积分吗?集群智能的基础只是作用于个体的运行准则和作用于整体的通用目标,这些目标通常还都很简单。可正是数量足够庞大的简单规则才孕育出了整体意义上的高级智能,这也验证了量变引发质变的哲学观点。
从抽象的角度来说,群体行为是大量自驱动个体的集体运动,每个自驱动个体都遵守一定的行为准则,当它们按照这些准则相互作用时就会表现出上述的复杂行为。群体本身不具备中心化的结构,而是通过个体之间的识别与协同达成稳定的分布式结构。这个分布式结构会随着环境的变化,以自身为参考系不断趋于新的稳定。集群智能(swarm intelligence)正是群居性生物通过协作表现出的自组织与分布式的宏观智能行为,它具有如下的特点:
第一个特点是可扩展性。广义的可扩展性意味着系统可以在增加体量的同时保持功能的稳定,而不需要重新定义其部件交互的方式。集群智能系统中的作用方式通常是个体间的间接通信,因而互动的个体数量往往不会随着群体中个体的总数量的增加而增长,每个个体的行为只受群体维度的松散影响。在人造的集群智能算法中,可扩展性保证了通过简单扩充来增强算法性能的可行性,而不需要重新编程。
第二个特点是并行性。集群智能系统天然具有并行性,这是因为组成集群的个体完全可以同时在不同的地方执行不同的行为。在人造的集群智能算法中,并行性能够增强系统的灵活性,能够在同时处理复杂任务不同方面的集群中自行组织。同时,并行性也决定了集群智能具有较强的环境适应能力和较强的鲁棒性(Robust),不会由于若干个体出现故障而影响群体对整个问题的求解。
第三个特点是容错性。去中心化和自组织的特点让容错性成为集群智能系统的固有属性。由于集群系统由许多可以互换的个体组成,他们中没有一个总司令负责控制整个系统的行为,所以一个失败的个体很容易被另一个完全正常运作的个体所取代。除此之外,去中心化的特性也大大降低了系统全面崩溃的可能性。
用集群智能方法实现人工智能,代表的是研究方式的转变。不管是人工神经网络还是深度学习,其本质都是对人类思维的功能模拟,采用的方法论是机械论的哲学,而机械论中先验规则设定的前提决定了功能模拟的方式很难产生人类水平的智能。既然机械论这条路走不通,研究者们便开始转向另一条可能的道路:从结构模拟出发,通过人为创造类似人类脑神经系统的结构模型,实现智能的大规模涌现。功能模拟的任务是重新制造出类人脑的复杂系统,结构模拟的任务则是复制出人脑这个复杂系统。一般来说,复制的难度要低于制造的难度。二进制的计算机可以通过算法代替人类执行特定的任务,但算法的核心问题也恰恰在于只能执行特定的任务,而不具备通用性,想要生成人类思维的特质,比如创造力和想象力,更是绝无可能。
结构模拟的理论基础在于对复杂系统的认识。当构成一个系统的基本单元数量极为庞大时,将这些个体看作一个整体,就会有一些全新的属性、规律或模式自发地冒出来,这种现象就称为“涌现”(emergence)。对于涌现现象来说,大量微观层次上的交互导致对其功能性的描述过于困难,结构化的模拟反倒成为一种直观有效的方式。对涌现现象的代表性应用,就是以蚁群算法为代表的各类粒子群算法。
在蚁群系统中,单只蚂蚁便是构成这一复杂系统的基本单元。在单只蚂蚁活动范围受限的情况下,整个蚁群中不同蚂蚁之间的协作与联动,却能够很快找到一条将食物搬回巢穴的最优路径。更重要的是,这一行为完全是自组织的行为,并不存在一个上帝视角的蚁后如元帅般指挥蚂蚁们的行动轨迹,这条最优线路完全是自发找到的。蚁群的行为给善于向自然学习的人类以新的启发:只对单只蚂蚁的简单行为进行建模,系统中不同蚂蚁间复杂的大规模互动过程交给蚂蚁自己完成,这样能否产生“涌现”的效果呢?
基于这样的想法,意大利米兰理工学院的马可·多里戈博士在他的博士论文中提出了蚁群优化算法(ant colony optimization):通过对蚁群在寻找食物过程中发现最优路径行为的模拟来寻找问题的最优解。蚁群算法的初始化是让第一批蚂蚁随机出发,独立且并行地搜索问题的解,对解的搜索就是蚂蚁对路径的选择。在行进的过程中,蚂蚁会在自己的路径上释放信息素,信息素的强度是与解的最优程度成正比的,新的蚂蚁则会根据已有信息素的强度选择自己的行进路径。
随着搜索的不断进行,信息素也会发生动态变化:旧蚂蚁留下的信息素会不断蒸发,新蚂蚁经过后则会产生新的信息素。蚁群的集群化搜索会产生聚集作用,最优路径会被越来越多的蚂蚁发现,信息素的强度也会逐渐增大,从而将更多蚂蚁吸引过来,被下一只蚂蚁选择的概率也就进一步增加。蚁群算法就是利用这种正反馈机制逐步遍历解空间,使搜索向最优解推进。在不断的实践中,蚁群算法不仅被证明是个相当靠谱的优化算法,还激发出了鸟群、蜂群等其他类似原理的最优化算法。当然,蚁群算法也有它的限制条件:只有当基本单元的数量足够巨大时,“涌现”的结果才会出现。当蚂蚁数目太少的时候是达不到“涌现”效果的。
蚁群的行为与蚁群算法的诞生对人工智能的研究也是一种启示:相对于宏观的功能模拟,结构模拟重于微观的解构。功能模拟是个自顶向下的过程:先确定要完成的任务,再来设计任务实现的方式。结构模拟则是个自底向上的过程:只对最底层的基本单元及其运作方式进行定义,并让这些基本单元在微观层面上进行交互,从而自发地生成各种宏观行为。在这个过程中,结构模拟回避了复杂系统中复杂性形成的过程,以放任自流的方式让微观单元自己完成。这未尝不是个好办法:当现有的技术水平远远不足以透彻地研究复杂系统时,与其通过功能模拟人为地对其运作方式进行武断地判断,不如采用无为而治的方式,发挥基本单元的自然天性,看看它能造出个什么世界。
接下来,我将分享人工智能---迁移学习与知识图谱


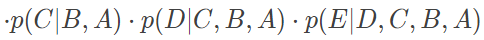
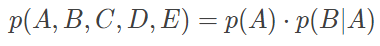

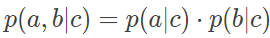
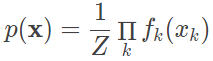



发表评论